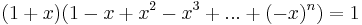Quasiregular element

This article addresses the notion of quasiregularity in the context of ring theory, a branch of modern algebra. For other notions of quasiregularity in mathematics, see the disambiguation page quasiregular.

In mathematics, specifically ring theory, the notion of quasiregularity provides a computationally convenient way to work with the Jacobson radical of a ring.^[1] Intuitively, quasiregularity captures what it means for an element of a ring to be "bad"; that is, have undesirable properties.^[2] Although a "bad element" is necessarily quasiregular, quasiregular elements need not be "bad," in a rather vague sense. In this article, we primarily concern ourselves with the notion of quasiregularity for unital rings. However, one section is devoted to the theory of quasiregularity in non-unital rings, which constitutes an important aspect of noncommutative ring theory.

1 Definition
2 Examples
3 Properties
4 Notes
5 References
6 See also

Definition

Let R be a ring (with unity) and let r be an element of R. Then r is said to be quasiregular, if 1 - r is a unit in R; that is, invertible under multiplication.^[1] The notions of right or left quasiregularity correspond to the situations where 1 - r has a right or left inverse, respectively.^[1]

An element x of a non-unital ring is said to be right quasiregular if there is y such that 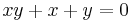$xy %2B x %2B y = 0$ .^[3] The notion of a left quasiregular element is defined in an analogous manner. The element y is sometimes referred to as a right quasi-inverse of x.^[4] If the ring is unital, this definition quasiregularity coincides with that given above. If one writes 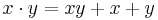$x \cdot y = xy %2B x %2B y$ , then this binary operation $\cdot$ is associative. Therefore, if an element possesses both a left and right quasi-inverse, they are equal.^[5]

Examples

If R is a ring, then the additive identity of R is always quasiregular
If 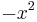$-x^2$ is right (resp. left) quasiregular, then $x$ is right (resp. left) quasiregular.^[6]
If R is a ring, every nilpotent element of R is quasiregular. This fact is also supported by an elementary computation:

If 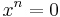$x^n = 0$ , then

$(1%2Bx)(1 - x %2B x^2 - x^3 %2B ... %2B (-x)^n) = 1$

A matrix is quasiregular in a matrix ring if it does not possess -1 as an eigenvalue. More generally, a bounded operator is quasiregular if -1 is not in its spectrum.
In a unital Banach algebra, if 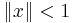$\|x\| < 1$ , then the geometric series 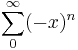$\sum_0^\infty (-x)^n$ converges. Consequently, every such x is quasiregular.
If R is a ring and S=R[[X₁,...,X_n]] denotes the ring of formal power series in n intederminants over R, an element of S is quasiregular if and only its constant term is quasiregular as an element of R.

Properties

Every element of the Jacobson radical of a (not necessarily commutative) ring is quasiregular.^[7] In fact, the Jacobson radical of a ring can be characterized as the unique right ideal of the ring, maximal with respect to the property that every element is right quasiregular.^[8]^[9] However, a right quasiregular element need not necessarily be a member of the Jacobson radical.^[10] This justifies the remark in the beginning of the article - "bad elements" are quasiregular, although quasiregular elements are not necessarily "bad." Elements of the Jacobson radical of a ring, are often deemed to be "bad."

If an element of a ring is nilpotent and central, then it is a member of the ring's Jacobson radical.^[11] This is because the principal right ideal generated by that element consists of quasiregular (in fact, nilpotent) elements only.

If an element, r, of a ring is idempotent, it cannot be a member of the ring's Jacobson radical.^[12] This is because idempotent elements cannot be quasiregular. This property, as well as the one above, justify the remark given at the top of the article that the notion of quasiregularity is computationally convenient when working with the Jacobson radical.^[1]

Notes

^ ^a ^b ^c ^d Isaacs, p. 180
^ Isaacs, p. 179
^ Kaplansky, p. 85
^ Polcino & Sehgal (2002), p. 298.
^ Since 0 is the multiplicative identity, if 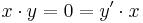$x \cdot y = 0 = y' \cdot x$ , then $y = (y' \cdot x) \cdot y = y' \cdot (x \cdot y) = y'$ . Quasiregularity does not require the ring to have a multiplicative identity.
^ Kaplansky, p. 108
^ Isaacs, Theorem 13.4(a), p. 180
^ Isaacs, Theorem 13.4(b), p. 180
^ Isaacs, Corollary 13.7, p. 181
^ Isaacs, p. 181
^ Isaacs, Corollary 13.5, p. 181
^ Isaacs, Corollary 13.6, p. 181

References

I. Martin Isaacs (1993). Algebra, a graduate course (1st ed.). Brooks/Cole Publishing Company. ISBN 0-534-19002-2.
Irving Kaplansky (1969). Fields and Rings. The University of Chicago Press.
Milies, César Polcino; Sehgal, Sudarshan K. (2002). An introduction to group rings. Springer. ISBN 9781402002380.